Paduri de Multimi Disjuncte

autor: Bogdan Iordache

Consideram urmatoarea problema: Se dau $N$ multimi de numere, initial fiecare multime $i$ continand un singur element, mai exact elementul $i$ . Asupra acestor multimi se efectueaza urmatoarele tipuri de operatii:

JOIN(x, y): daca valorile $x$ si $y$ nu se afla in aceeasi multime, sa se reuneasca multimea lui $x$ si multimea lui $y$
QUERY(x, y): sa se raspunda cu “DA” sau “NU” daca valorile $x$ si $y$ se afla in aceeasi multime.

Exemplu:

N = 4; initial multimile sunt: {1}, {2}, {3}, {4}
JOIN(1, 2)  => {1, 2}, {3}, {4}
JOIN(3, 4)  => {1, 2} {3, 4}
QUERY(1, 3) => NU (1 si 3 nu sunt in aceeasi multime)
QUERY(1, 2) => DA (1 si 2 sunt in aceeasi multime)
JOIN(1, 3)  => {1, 2, 3, 4}
QUERY(2, 4) => DA
JOIN(2, 3)  => {1, 2, 3, 4} (nu se intampla nimic)

Pentru a retine structura multimilor disjunte ne putem folosi de o multime de arbori (de aici termenul de “padure”). Spre exemplu, daca consideram multimea $\{1,2,3,4,5,6,7,8\}$ cu submultimile disjunte $\{1, 3, 4\}$ , $\{2,5,7\}$ si $\{6, 8\}$ , o posibila structura a arborilor este urmatoarea:

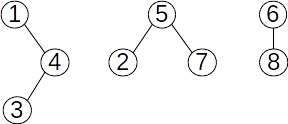
enter image description here
Cum putem salva o astfel de structura in memorie? Folosind un vector de parinti ( $T[i] = j$ daca $j$ este parintele lui $i$ in arbore, sau $T[i]=0$ daca $i$ este radacina de arbore).

Pentru exemplul de mai sus vectorul de parinti ar fi $[0, 5, 4, 1, 0, 0, 5, 6]$ .

Acum sa presupunem ca vrem sa reunim multimea lui $8$ cu multimea lui $7$ . Acest lucru il vom face unind radacina arborelui din care face parte $8$ cu radacina arborelui din care face parte $7$ . Pentru a determina radacina arborelui din care face parte un nod, putem folosi urmatoarea functie:

int get_root(int node) {
	while (T[node] > 0)  // mergem din parinte in parinte
		node = T[node];
	return node;
}

Determinam astfel ca radacina pentru $7$ este $5$ , iar pentru $8$ este $6$ . Alipirea o putem face usor prin atribuirea T[6] = 5, obtinand structura urmatoare:

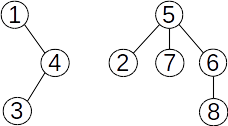
enter image description here
Nu am specificat inca la operatia JOIN care dintre radacini este alipita celeilalte. Pentru a obtine complexitatea optima vom lega mereu radacina arborelui cu mai putine noduri de radacina arborelui cu mai multe noduri (vom demonstra mai tarziu).

Pentru simplificarea implementarii vom salva in T[i], daca i este radacina, numarul de noduri din arborele cu radacina in i (cu semnul $-$ , pentru a deosebi aceasta valoare de valorile efective ale parintilor). Deci vectorul de parinti pentru ultima structura de arbori ar fi: $[-3, 5, 4, 1, -5, 5, 5, 6]$ .

Functia get_root ramane neschimbata, iar operatia JOIN o putem implementa astfel:

void join(int x, int y) {
	int root_x = get_root(x);  // radacina arborelui lui x
	int root_y = get_root(y);  // radacina arborelui lui y
	if (root_x == root_y)  // sunt deja in acelasi arbore
		return;
	if (T[root_x] <= T[root_y]) {  // arborele lui x are mai multe noduri
		T[root_x] += T[root_y];
		T[root_y] = root_x;  // legam arborele lui y de arborele lui x
	} else {
		T[root_y] += T[root_x];
		T[root_x] = root_y;  // legam arborele lui x de arborele lui y
	}
}

Iar pentru QUERY:

bool query(int x, int y) {
	// x si y sunt in acelasi arbore daca au aceeasi radacina
	return get_root(x) == get_root(y);
}

Complexitatea acestor operatii este strict legata de numarul de iteratii efectuate de functia get_root (adancimea la care se afla nodul in arbore). Vom incerca sa construim un caz in care numarul de iteratii este cat mai mare posibil.

Plecam de la un singur nod (initial singur in arbore). Functia get_root apelata pentru acest nod se opreste dupa o iteratie. Pentru a duce nodul nostru la adancime $2$ , trebuie ca arborele sau sa fie legat de un alt arbore in urma unui JOIN. Dar un arbore poate fi legat doar de un arbore cu cel putin la fel de multe noduri, deci va trebui legat de un arbore cu minim un nod.

Acum nodul nostru se afla la adancime $2$ intr-un arbore cu minim $2$ noduri. Pentru a mai creste adancimea cu o unitate trebuie ca acest arbore sa fie legat de un altul, care are deci cel putin $2$ noduri (trebuie sa fie cel putin la fel de “greu”).

Continuand rationamentul, cand nodul va ajunge la adancime $k$ se va afla intr-un arbore cu minim $2^k$ noduri. Dar noi avem $N$ noduri in total, deci $k$ nu poate depasi $log_2N$ . Ajungem la concluzia ca pentru toate operatiile definite complexitatea este $O(log\ N)$ .

O alta optimizare pe care o putem face tine tot de functia get_root. Odata ce parcurgem lantul de la nodul cu care a fost apelata functia, pana la radacina, putem lega toate nodurile de pe drum direct la radacina. De acum inainte, la orice apel al functiei get_root pentru oricare dintre aceste noduri, dintr-un singur pas ajungem la radacina (mult mai repede).

Mai jos aveti un exemplu de compresie a drumului dupa un apel de get_root facut pentru nodul $7$ :
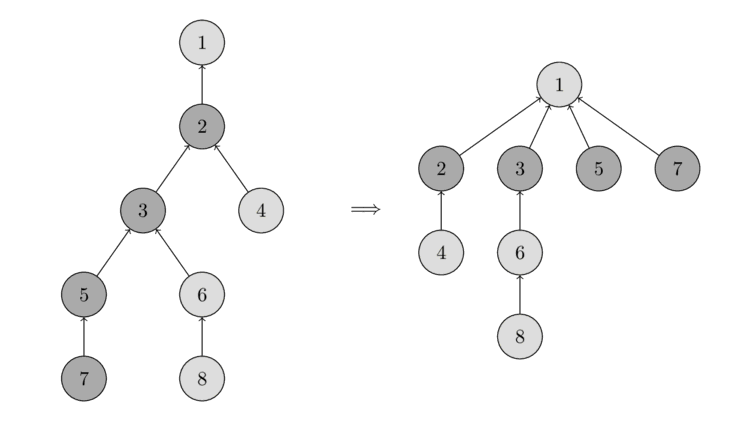
enter image description here
Pentru a realiza aceasta optimizare functia get_root devine:

int get_root(int node) {
	int aux = node;
	while (T[node] > 0)
		node = T[node];
	int root = node;
	// mai parcurg odata acelasi drum si unesc nodurile de root
	node = aux;
	while (node != root) {
		aux = T[node];
		T[node] = root;
		node = aux;
	}
	return root
}

Aceasta optimizare duce complexitatea medie a tuturor operatiilor la $O(log^*N)$ , unde $log^*$ se numeste logaritmul iterat, care pentru valori rezonabile ale lui $N$ (zeci de milioane) nu depaseste valoarea $5$ .

Problema echivalenta

Consideram un graf cu $N$ noduri. Avem update-uri de forma: (a, b): se adauga o muchie de la nodul a la nodul b si query-uri de forma (a, b): sunt a si b in aceeasi componenta conexa?

Problema se rezolva cu ajutorul padurilor de multimi disjuncte. Multimea corespunde acum unei componente conexe. Update-ul este de fapt un JOIN in care reunim componentele conexe ale lui a si b, iar query-ul este acelasi ca mai devreme.

NOTÁ BÉNE

Tehnica de a lega arborele mai “usor” de arborele mai “greu” (ca numar de noduri) mai poarta numele de “reuniune dupa greutate”. In alte variante de implementare ale algoritmului puteti intalni notiunea de “reuniune dupa rang”. Rangul unui arbore reprezinta adancimea maxima a unei frunze, iar la JOIN se leaga arborele cu rang mai mic de arborele cu rang mai mare. Doar atunci cand arborii au acelasi rang, dupa unire, radacina rezultata va capata un rang mai mare cu $1$ . Complexitatea operatiilor ramane aceeasi, iar demonstratia pentru complexitatea $O(logN)$ (adica fara compresia drumului) este foarte asemanatoare, de aceea va propun sa o realizati singuri :)

Probleme propuse

1. Bile (infoarena)

Structura bilelor poate fi vazuta ca un graf, in care bilele de pe masa sunt noduri, iar muchiile corespund perechilor de bile adiacente pe linie sau coloana.

In problema, la fiecare pas se elimina un nod impreuna cu muchiile adiacente si suntem intrebati cate componente conexe are graful rezultat. Pusa astfel, problema este foarte dificila, insa avem un avantaj: putem raspunde la intrebari in orice ordine dorim, iar la final le afisam in ordinea ceruta.

Ideea care ne aduce solutia este sa procesam toate operatiile in ordine inversa, cu alte cuvinte in loc sa avem operatii de eliminare a bilelor, adaugam bile.

Pornim de la masa goala (fara nicio bila), iar la fiecare pas o bila este adaugata la pozitia $(i, j)$ , ne uitam la cei $4$ vecini ai pozitiei actuale si in cazul in care avem deja bile acolo adaugam muchie intre nodurile corespunzatoare bilei noi si vecinei sale. Putem mentine componentele conexe folosind paduri de multimi disjunte. Complexitatea solutiei este $O(N^2log^*N)$ .

Ca indicatie de implementare, putem identifica nodurile prin linia si coloana matricei. Puteti salva structura de paduri astfel:

pair<int, int> T[MAXN][MAXN];  // salveaza parintii
int SZ[MAXN][MAXN];            // dimensiunea arborelui cu radacina (i, j)

2. Banana (infoarena)

Problema ne cere sa determinam cele mai mari $K$ componente conexe ale grafului de bananieri. Putem deci folosi paduri de multimi disjuncte pentru a determina aceste componente, pe masura ce detectam muchiile dintre bananieri (doi bananieri au o muchie intre ei daca sunt adiacenti pe linie sau coloana).

Dificultatea sta in a determina care bananieri sunt adiacenti, intrucat limitele nu ne permit sa mentinem o matrice. Putem insa sa sortam bananierii dupa linie si in caz de egalitate dupa coloana, determinand usor bananierii adiacenti pe orizontala. Asemanator putem determina si bananierii vecini pe verticala printr-o alta sortare.

Complexitatea finala este $O(NlogN)$ din cauza celor doua sortari.

3. Secvmax (infoarena)

Prima observatie este ca putem rezolva query-urile in orice ordine dorim, iar la final sa afisam raspunsul pentru toate. Veti mai auzi expresia: rezolvam query-urile offline.

Vom sorta toate query-urile crescator dupa $Q$ si separat vom sorta si toate valorile din sir crescator. Consideram graful in care nodurile sunt pozitiile din sir, iar muchii pot exista doar intre pozitii adiacente.

Parcurgem query-urile in ordinea sortarii. Fie $Q$ valoarea pentru query-ul curent. Consideram active toate pozitiile cu valori mai mici sau egale decat $Q$ . Valorile mai mici decat query-ul anterior sunt deja active, deci la acest pas activam si valorile mai mari decat query-ul anterior dar mai mici sau egale decat $Q$ (de aceea am determinat si sortarea valorilor din sir).

Activarea unei pozitii inseamna sa adaugam nodul pozitiei in graf si sa adaugam muchiile catre vecinii sai activi (aproape identic cu operatia de adaugare de la problema Bile). Folosim paduri de multimi disjuncte pentru mentine componentele conexe si dimensiunile lor.

Dupa ce am activat nodurile de la pasul pentru query-ul $Q$ , componentele conexe nu sunt altceva decat intervalele compacte ce contin valori $\leq Q$ , deci putem spune imediat care este intervalul de lungime maxima.

Complexitate: $O(NlogN + MlogM)$ de la sortari.

4. Curcubeu (infoarena)

Vom considera colorarile incepand cu ultima. Fie $C_i$ culoarea curenta. Parcurgem intervalul asociat ei si de fiecare data cand gasim o casuta necolorata ii asociem valoarea $C_i$ . Aceasta solutie are complexitatea $O(N^2)$ si obtine in jur de $20$ de puncte.

Analizand solutia anterioara, observam ca vom parcuge de foarte multe ori casute deja colorate, lucru inutil si consumator de timp.

Pentru fiecare pozitie $i$ vom mentine o valoare $Next[i]$ , semnficand faptul ca intervalul $[i, Next[i]-1]$ contine doar casute colorate (ca initializare, cand nu avem nicio casuta colorata inca, $Next[i] = i$ ). Astfel, la colorarile urmatoare, vom putea “sari” peste secvente intregi de pozitii anterior colorate.

Indicatii de implementare:

int left[MAXN], right[MAXN], C[MAXN]; // datele despre colorari
int Next[MAXN]; // cu semnificatia de mai sus
...
int find_next(int pos) {
	// gaseste prima pozitie la dreapta lui pos care nu este colorata
	int aux = pos;
	// mergem din Next in Next pana ajungem la o pozitie necolorata
	while (Next[pos] != pos)
		pos = Next[pos];
	// cand ajungem la pos == Next[pos] inseamna ca pos nu este colorata
	int res = pos;
	pos = aux;
	// legam toate pozitiile prin care am trecut direct
	// de prima pozitie necolorata determinata
	while (Next[pos] != res) {
		aux = Next[pos];
		Next[pos] = res;
		pos = aux;
	}
	return res;
}

void solve() {
	// initial toate pozitiile sunt necolorate
	for (int i = 1; i <= N; i++)
		Next[i] = i;
	for (int i = N - 1; i > 0; i--) {
		for (int j = find_next(left[i]); j <= right[i]; j = Next[j]) {
			solutie[j] = C[i];
			// l-am colorat pe j, cautam urmatoarea pozitie necolorata
			Next[j] = find_next(j + 1);
		}
	}
	
}

Observam ca find_next implementeaza metoda de compresie a drumului, pe care am intalnit-o mai devreme la padurile de multimi disjuncte. Astfel complexitatea acestei implementari se amortizeaza la $O(Nlog^*N)$ .

5. Jstc (infoarena)

Solutia acestei probleme se aseamana cu rezolvarea problemei Curcubeu, de aceea va recomand sa abordati acea problema inainte.

Prima observatie necesara in rezolvarea problemei este faptul ca stiva este intotdeauna crescatoare.

A doua observatie este ca raspunsul pentru un anumit numar $x$ poate doar sa creasca dupa diferite operatii de tip insert sau erase (el poate sa fie si $-1$ dar acesta este un caz particular usor de rezolvat). Daca raspunsul la momentul actual este $y$ ( $y$ fiind cel mai mic numar din stiva, mai mare sau egal cu $x$ ), mai tarziu se vor adauga in stiva doar valori mai mari, iar daca cumva $y$ este eliminat, raspunsul nu poate deveni decat mai mare.

Vom volosi inca o data tehnica de compresie a drumurilor de la padurile de multimi disjuncte. Vom tine pentru fiecare numar $x$ , care poate aparea la query, $Next[x]$ ce reprezinta un numar mai mare ca $x$ dar care sigur nu sare de urmatorul numar mai mare ca $x$ ce se afla momentan in stiva. Conform celei de-a doua observatii, $Next[x]$ poate doar sa creasca in urma diverselor operatii.

Acum pentru a cauta raspunsul si anume primul numar din stiva mai mare sau egal cu $x$ vom parcurge pe rand $Next[x]$ , $Next[Next[x]]$ , $Next[Next[Next[x]]]$ , $\ldots$ pana cand gasim un numar care se afla in stiva (asemanator cu problema Curcubeu, putem retine aceasta informatie avand $Next[x] = x$ , daca $x$ se afla in stiva).

Tot conform celei de a doua observatii, putem acum sa modificam valorile $Next[x]$ , $Next[Next[x]]$ , $Next[Next[Next[x]]]$ , $\ldots$ in raspunsul pentru intrebarea $x$ . Astfel drumurile se vor “compacta” si nu vom parcurge de prea multe ori aceleasi drumuri.

Obtinem astfel complexitatea de $O(log^*N)$ per query, unde cu $N$ am notat valoarea maxima inserata in stiva ( $\leq 10^6$ ).

6. Egal (infoarena)

Pentru a rezolva aceasta problema avem nevoie mai intai sa introducem/recapitulam structura de date hash map, implementata in biblioteca standard STL in clasa unordered_map (detalii aici).

Un “map” este de fapt un dictionar ce contine chei, carora le sunt asociate valori. Exemplu:

{
	cheie_1: valoare_1,
	cheie_2: valoare_2,
	...
}

Un hash map permite urmatoarele operatii in complexitate constanta, aproximativ $O(1)$ :

adauga o cheie noua la dictionar cu o anumita valoare
schimba valoarea pentru o anumita cheie
verifica daca o cheie anume exista in dictionar
sterge o cheie din dictionar impreuna cu valoarea ei

In C++ putem defini un hash map astfel:

#include <unordered_map>
using namespace std;
...
unordered_map<T1, T2> hm;

Unde T1 si T2 sunt tipurile de date asociate cheilor, respectiv valorilor. T2 poate fi orice tip de date oricat de complex (int, char*, vector<vector<int>>, s.a.m.d.), in timp ce T1 trebuie sa fie un tip pentru care o functie de hash exista implementata. Puteti furniza si voi o astfel de functie pentru orice tip doriti, dar aceste detalii depasesc scopul acestui material. STL are deja functii hash preimplementate pentru tipuri standard (numere intregi int, long long, siruri de caractere reprezentate prin clasa string, etc.)

Pentru a demonstra cum putem folosi unordered_map, vom realiza urmatoarele operatii pe un hash map cu chei de tip string si valori de tip int:

insereaza cheia “abc” cu valoarea 5, cheia “def” cu valoarea 7, cheia “foo” cu valoarea -5
schimba valoarea cheii “foo” in 20
afiseaza valoarea cheii “def”
sterge cheia “abc” din dictionar
verifica faptul ca “abc” nu mai este in dictionar
afiseaza toate perechile cheie-valoare

#include <unordered_map>
#include <string>
#include <iostream>
using namespace std;
...
unordered_map<string, int> hm;
...
// adaugam chei si valori la dictionar
hm["abc"] = 5;
hm["def"] = 7;
hm["foo"] = -5;
// schimbam valoarea asociata unei chei
hm["foo"] = 20;
// accesam valoarea unei chei
cout << hm["def"];
// stergem o cheie din dictionar
hm.erase("abc");
// afisam daca "abc" mai este in dictionar
cout << hm.count("abc"); // afiseaza 0
// parcurgem toate perechile cheie valoare si le afisam
for (const pair<string, int>& p : hm)
	cout << p.first << "->" << p.second << "\n";

Ne intoarcem acum la problema Egal.
Problema se poate rezolva prinr-o simpla parcurgere in adancime (DFS), in care de fiecare data cand terminam de parcurs subarborele unui nod si ne intoarcem din recursivitate vrem sa avem calculat atat un dictionar care contine pentru fiecare cheie prezenta in subarbore numarul ei de aparitii, cat si care este cheia ce apare de cele mai multe ori in subarbore.

Pentru frunze, dictionarul contine doar cheia din frunza, iar valoarea asociata este $1$ .

Pentru orice alt nod, putem initializa dictionarul sau introducand cheia sa cu valoarea asociata $1$ . Parcurgem acum fiii dictionarului si apelam recursiv pentru fiecare functia DFS. Cand ne intoarcem dintr-un fiu, cunoastem deja dictionarul asociat subarborelui sau. Ramane sa reunim dictionarul curent al parintelui cu dictionarul fiului. Pentru a face acest lucru eficient, vom parcurge dictionarul mai mic (cu mai putine chei) si vom updata cu valorile acestuia dictionarul mai mare. Astfel vom face un numar de operatii direct proportional cu dimensiunea dictionarului mai mic. Maximul curent va fi fie maximul de dinainte de a procesa acest fiu, fie una din cheile actualizate de acest fiu. Continuam apoi cu restul fiilor.

Ce complexitate are aceasta solutie? Pentru a raspunde trebuie mai intai sa obervam ca dimensiunea maxima posibila a unui dictionar calculat pentru un subarbore este chiar dimensiunea subarborelui.

Complexitatea poate fi determinata numarand cate operatii de “mutare” a unor valori dintr-un dictionar in altul se efectueaza. Vom urmari cheia asociata unei frunze si vom incerca sa o mutam de cat mai multe ori dintr-un dictionar in altul.

Este clar ca pentru a fi mutata din dictionarul curent, trebuie ca acesta sa fie reunit cu un dictionar cel putin la fel de mare. Astfel la prima mutare trebuie reunit cu un dictionar de dimensiune minim $1$ , apoi cu unul de dimensiune minim $2$ , apoi minim $4$ s.a.m.d. Insa stim ca aceste dictionare nu pot avea dimensiunea mai mare decat $N$ (numarul de valori), deci in concluzie aceasta cheie nu poate fi mutata de mai mult de $O(logN)$ ori.

Obtinem complexitatea finala: $O(NlogN)$ .

Atentie! Atunci cand reuniti dictionarul nodului curent cu dictionare ale fiilor, nu faceti direct atribuiri de map-uri, intrucat complexitatea unei atribuiri este proportionala cu dimensiunea dictionarului.

O modalitate de a implementa corect este sa alocam de la inceput cate un map pentru fiecare nod, si o lista de indici care indica pentru fiecare nod care este map-ul sau, iar in cazul in care trebuie sa actualizam map-ul fiului cu valorile din map-ul nodului curent, vom schimba indicele asociat nodului curent pentru a indica faptul ca de acum map-ul sau este map-ul acelui fiu.

unordered_map<int, int> hm[MAXN];
int indice[MAXN];
...
// initial
for (int i = 1; i <= N; ++i)
	indice[i] = i; // nodul i are asocial map-ul i
...
// vrem sa reunim map-ul lui nod cu map-ul lui fiu
hm[indice[nod]]; // map-ul lui nod
hm[indice[fiu]]; // map-ul fiului
// daca "varsam" valorile din map-ul fiului in map-ul nodului
//   indice[nod] ramane neschimbat
// altfel
indice[nod] = indice[fiu]; // acum map-ul nodului este map-ul fiului

O solutie mai eleganta se poate obtine folosind pointeri. De fapt, solutia de mai sus doar simuleaza intr-un mod rudimentar modul de functionare al memoriei si adresarea prin pointeri. O astfel de implementare gasiti aici.

7. Luff (infoarena)

Un query $(nod, k)$ , se traduce in “Care este valoarea maxima VAL pentru care daca pastram in graf doar muchiile de cost $\geq$ VAL, nodul $nod$ face parte dintr-o componenta conexa cu minim $k$ noduri?”

La aceasta problema vom rezolva query-urile offline (asa cum am mai facut la problemele anterioare). Putem de la inceput sa sortam query-urile descrescator. Pornim de la graful cu $N$ noduri si nicio muchie.

Pornim deci cu $N$ componente conexe cu cate un nod. Pentru fiecare componenta conexa retinem intr-o structura toate query-urile asociate nodurilor din componenta conexa si care nu au fost inca rezolvate.

Adaugam muchiile pe rand in ordinea sortarii. Atunci cand adaugam o muchie exista posibilitatea ca doua componente conexe sa fie reunite in una singura. Trebuie in primul rand sa reunim multimile query-urilor corespunzatoare celor doua componente si sa rezolvam dintre acestea pe cele pe care le putem. Query-urile care pot fi rezolvate sunt cele pentru care $k$ este mai mic sau egal cu dimensiunea noii componente conexe.

De aici se contureaza urmatoarea idee de implementare: componentele conexe le putem mentine folosind structura de paduri de multimi disjunte, iar pentru fiecare componenta conexa retinem o structura ce poate mentine eficient query-urile astfel incat sa putem interoga rapid care este query-ul cu $k$ minim. O astfel de structura poate fi fie un set, fie un heap/priority_queue. Aceste structuri de date ne permit in $O(logQ)$ sa adaugam elemente, sa aflam care este elementul minim si sa il putem elimina.

Atunci cand adaugam o muchie ce uneste doua componente conexe, legam radacina arborelui mai mic din padure de radacina arborelui mai mare, apoi mutam toate query-urile din structura retinuta pentru componenta mai mica in structura corespunzatoare componentei mai mari.

Acum putem extrage din structura query-ul cu $k$ minim, iar daca $k$ este mai mic decat dimensiunea noii componente conexe putem raspunde la acel query. Cat timp putem rezolva query-ul minim din structura, il rezolvam, il eliminam din structura, si continuam cu urmatorul minim. Query-urile ramase vor fi rezolvate mai tarziu. Raspunsul la query-urile rezolvate la acest pas este costul muchiei tocmai adaugate.

Mutarea unui query dintr-o structura in alta are cost $O(logQ)$ (din cauza set-ului/heap-ului). Un query este mutat dintr-o structura in alta atunci cand componenta sa conexa este reunita cu o componenta mai mare. Din demonstratia complexitatii padurilor, stim ca acest lucru nu se poate intampla de mai mult de $O(logN)$ ori. Deci numarul de operatii de mutare este $O(QlogN)$ .

In concluzie, complexitatea finala este $O(Q\cdot logQ\cdot logN + M\cdot log^*N)$ , corespunzatoare operatiilor de mutare a query-urilor si padurilor de multimi disjuncte.

Detaliile de implementare le puteti consulta aici.