Lowest Common Ancestor

autor: Bogdan Iordache

Definitie

Fie $T$ un arbore cu radacina, si $x$ si $y$ doua noduri din $T$. Numim “cel mai apropiat stramos comun”/“lowest common ancestor” (i.e. LCA) al nodurilor $x$ si $y$ acel nod $z$ cu proprietatea ca $z$ este stramos al lui $x$ si al lui $y$ si este nodul de adancime maxima din $T$ cu aceasta proprietate.

Exemplu

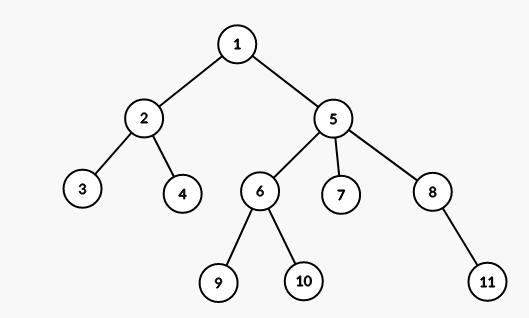
Notam LCA(x, y) cel mai apropiat stramos comun al nodurilor x si y.
Vom considere, pentru simplitate, si fara a restrange generalitatea, ca toti arborii vor avea ca radacina nodul 1.

In figura de mai sus:

• LCA(3, 4) = 2
• LCA(10, 11) = 5
• LCA(4, 7) = 1
• LCA(7, 8) = 5
• LCA(9, 5) = 5

Explicatie pentru LCA(10, 11): exista doua noduri care sunt stramosi atat pentru 10 cat si pentru 11 (nodurile 1 si 5); dintrea acestea 5 are adancime maxima.

Obs. Un nod se considera stramos al lui insusi, deci daca x este stramos al lui y, atunci LCA(x, y) = x.

Exemple de aplicatii

1. O aplicatie evidenta este determinarea lungimii drumului minim dintre doua noduri x si y. Daca notam cu nivel[x] adancimea nodului x, avem lungimea drumului de la x la y:
   nivel[x] + nivel[y] - 2 * nivel[LCA(x, y)]
2. Aplicatiile practice sunt nenumarate, un exemplu din lingvistica istorica ar fi determinarea celui mai apropiat stramos a doua cuvinte din limbi diferite (cu alte cuvinte “care este cel mai recent cuvant din care au fost derivate ambele cuvinte date?”)
   

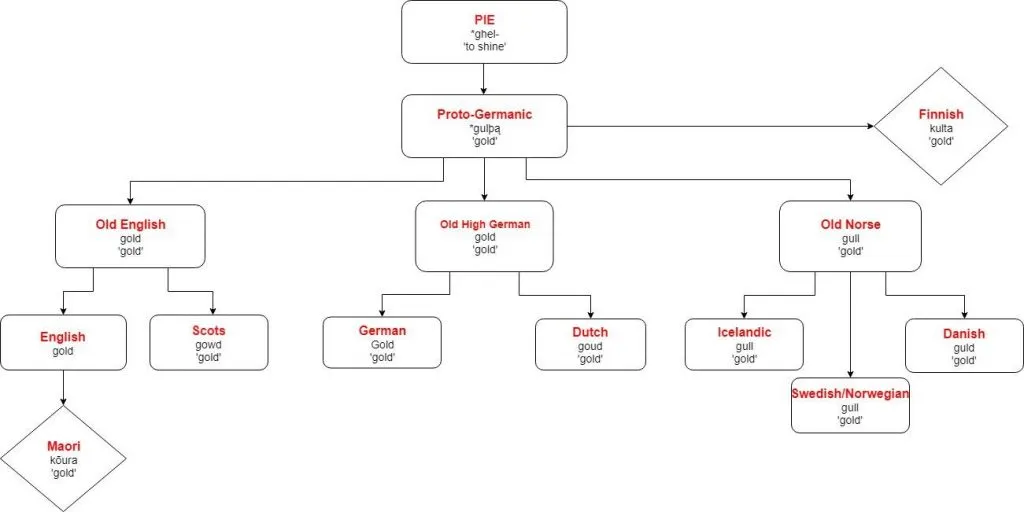
Algoritmi pentru determinarea LCA

Problema o putem defini in general astfel:

• avem un arbore cu $N$ noduri si radacina in nodul $1$;
• se dau $Q$ intrebari de forma $(x, y)$, determinati LCA(x, y).

Ca referinta vom folosi problema LCA (infoarena).

Complexitate $O(Q \cdot N)$

Aceasta solutie este o abordare simpla care functioneaza astfel:

• pentru o intrebare $(x, y)$ consideram fara a restrange generalitatea ca $x$ se afla la o adancima mai mare sau egala decat adancimea lui $y$;
• cat timp $x$ se afla la o adancime mai mare sau egala cu adancimea lui $y$, $x$ devine parintele lui $x$ din arbore (urcam cu cate un nivel)
• avand acum $x$ si $y$ la aceeasi adancime, cat timp sunt diferite vom “urca” ambele noduri cu cate un nivel ($x$ devine parintele lui $x$, iar $y$ devine parintele lui $y$).
• valoarea egala a lui $x$ si $y$ de la finalul iteratiilor de mai sus este LCA(x, y).

Notam cu parinte[i] parintele din arbore al nodului i.
Notam cu nivel[i] adancimea nodului i.
Notam cu arbore[i] lista de fii (descendenti directi) ai nodului i (implementata folosind std::vector din C++).

nivel se poate calcula usor printr-o parcurgere DF:

void dfs(int nod, int nvl = 1)
{
    nivel[nod] = nvl;
    for (int fiu : arbore[nod])
    {
        dfs(fiu, nvl + 1);
    }
}

Determinarea LCA-ului pentru doua noduri se poate implementa astfel:

int lca(int x, int y)
{
    if (nivel[x] < nivel[y])
    {
        swap(x, y);
    }
    while (nivel[x] > nivel[y])
    {
        x = parinte[x];
    }
    while (x != y)
    {
        x = parinte[x];
        y = parinte[y];
    }
    return x;
}

O implementare completa a acestei solutii puteti gasi aici.

Complexitate $O(N\log N + Q\log N)$

Liniarizarea arborelui

Pentru a putea explica aceasta solutie mai usor vom face o scurta precizare legata de parcurgerea DF a unui arbore.

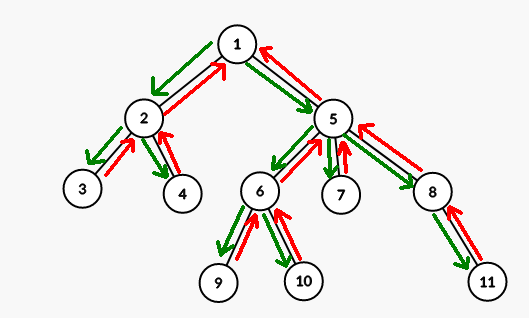
Notam intr-o lista nodurile prin care trecem (adaugam un nod atunci cand ajungem cu parcurgerea prima oara la el, si il mai adaugam atunci cand apelul recursiv pentru el ia sfarsit):
[1, 2, 3, 3, 4, 4, 2, 5, 6, 9, 9, 10, 10, 6, 7, 7, 8, 11, 11, 8, 5, 1]

Fiecare nod apare de exact 2 ori. Notam cu p_start[i] prima pozitie pe care apare nodul i in lista si cu p_end[i] ultima pozitie pe care apare i. Astfel pentru un nod i avem definit un interval [p_start[i], p_end[i]].

O observatie esentiala este ca pentru doua noduri x si y avem x stramos al lui y daca si numai daca intervalul lui x include intervalul lui y.

Putem determina liniarizarea de mai sus chiar in timpul pargurgerii DF:

int p_curent = 0, p_start[MAX_N], p_end[MAX_N];

void dfs(int nod, int nvl = 1)
{
    nivel[nod] = nvl;
    p_start[nod] = ++p_curent;
    for (int fiu : arbore[nod])
    {
        dfs(fiu, nvl + 1);
    }
    p_end[nod] = ++p_curent;
}

Si putem verifica usor daca un nod este stramos al altuia:

bool este_stramos(int x, int y)
{
    // return true <=> x este stramos al lui y
    return p_start[x] <= p_start[y] && p_end[y] <= p_end[x];
}

Problema “Stramosi” (infoarena)

Mentionam aceasta problema intrucat tehnica aplicata aici este esentiala pentru solutia noastra la problema determinarii LCA.

Pe scurt, problema cere pentru un nod $x$, care este al $k$-lea stramos al sau (pentru $k=1$ raspunsul este parintele lui $x$, pentru $k=2$ parintele parintelui lui $x$ s.a.m.d.).

O solutie la o astfel de intrebare in complexitate timp $O(k)$ este triviala (iteram din parinte in parinte de $k$ ori).

O solutie mult mai eficienta se realizeaza prin precalcularea urmatoarei tabele:
stramos[p][nod] := al $2^p$-lea stramos al nodului nod ($0$ daca nu exista un astfel de stramos).

Determinarea acestei tabele se poate realiza astfel:

void calculeaza_stramosi()
{
    for (int nod = 1; nod <= N; ++nod)
    {
        stramos[0][nod] = parinte[nod];
    }
    for (int p = 1; p < MAX_LOG; ++p)
    {
        for (int nod = 1; nod <= N; ++nod)
        {
            stramos[p][nod] = stramos[p - 1][stramos[p - 1][nod]];
        }
    }
}

Determinarea celui de-al $k$-lea stramos se reduce acum la scrierea lui $k$ in baza $2$:

int gaseste_stramos(int x, int k)
{
    for (int p = 0; p < MAX_LOG; p++)
    {
        if (k & (1 << p))
        {
	          x = stramos[p][x];
        }
    }
    return x;
}

“Stramosi” pentru LCA

Revenim acum la determinarea LCA. Fie nodurile $x$ si $y$ pentru care vrems a determinam LCA. Vom lasa la o parte cazurile in care fie $x$ este stramos al lui $y$, fie $y$ este stramos al lui $x$. Aceste cazuri pot fi verificate usor folosind functia este_stramos.

Ideea ce sta la baza solutiei este faptul ca putem cauta binar stramosul de adancime minima al lui $x$ care NU este stramos al lui $y$. Automat, aprintele acestui nod este stramosul comun de adancime maxima (LCA) al nodurilor $x$ si $y$.

Cautarea binara se poate face “pe biti” folosind tabela stramos:

int lca(int x, int y)
{
    if (este_stramos(x, y))
    {
        return x;
    }
    if (este_stramos(y, x))
    {
        return y;
    }
    for (int p = MAX_LOG - 1; p >= 0; --p)
    {
        int z = stramos[p][x];
        if (z != 0 && !este_stramos(z, y))
        {
            x = z;
        }
    }
    return stramos[0][x];
}

Cu alte cuvinte, fixam pe rand cate un bit (incepand cu cel mai semnificativ) al distantei de la $x$ pana la nodul de adancime minima care nu este stramos al lui $y$.

Complexitatea este data de calculul tabelei stramos, $O(N\log N)$ si de complexitatea functiei lca aplicata pentru fiecare interogare, $(Q\log N)$.

O implementare completa a acestei solutii puteti gasi aici.

Complexitate $O(N\log N + Q)$

!!! Pentru aceasta solutie avem nevoie de cunostinte legate de Range Minimum Query (RMQ).

Consideram parcurgearea DF de mai devreme:

Vom nota acum nodurile de fiecare data cand ajungem la ele (fie prima oara, fie la fiecare intoarcere din cate un fiu). De asemenea, retinem pentru fiecare nod si nivelul sau intr-un tabel.

nod	1	2	3	2	4	2	1	5	6	9	6	10	6	5	7	5	8	11	8	5	1
nivel	1	2	3	2	3	2	1	2	3	4	3	4	3	2	3	2	3	4	3	2	1

Notam cu p_start[i] prima pozitie din lista de mai sus pe care apare nodul i.

Fie acum doua noduri oarecare x si y. Intervalul dintre pozitiile p_start[x] si p_start[y] va contine cel putin o aparitie a nodului z = LCA(x, y) si, mai mult, niciun alt stramos comun al nodurilor x si y nu va aparea in acest interval.

Motivul este destul de usor de intuit: nodurile x si y sunt parcurse atunci cand DF-ul proceseaza subarborele lui z. Din momentul in care parcurgerea ajunge in z nu va mai parasi subarborele acestuia pana cand nu il viziteaza pe tot.

Am redus astfel acum problema determinarii LCA la o problema de minim pe interval din lista de mai sus. LCA(x, y) nodul de nivel minim din intervalul [p_start[x], p_start[y]] (considerand ca p_start[x] <= p_start[y]).

Cu alte cuvinte putem calcula o tabela RMQ si putem raspunde la astfel de intrebari in $O(1)$.

Ca detalii de implementare, vom retine o matrice rmq[p][i] care va contine nodul (alaturi de nivelul acestuia) cu nivel minim din intervalul de pozitii $[i, i + 2^p - 1]$.

Initializarea pentru rmq[0][i] se face inca de la inceput, la parcurgerea DF:

struct RmqItem
{
    int nod;
    int nvl;
};

int p_curent;
int p_start[2 * MAX_N]; // lista generata de parcurgerea DF are exact 2 * N - 1 pozitii
RmqItem rmq[MAX_LOG][2 * MAX_N];

void dfs(int nod, int nvl = 1)
{
    rmq[0][++p_curent] = {nod, nvl};
    p_start[nod] = p_curent;
    for (int fiu : arbore[nod])
    {
        dfs(fiu, nvl + 1);
        rmq[0][++p_curent] = {nod, nvl};
    }
}

Calculul restului de linii se face folosind algoritmul clasic pentru RMQ:

void calculeaza_rmq()
{
    for (int p = 1; p < MAX_LOG; ++p)
    {
        for (int i = 1; i <= p_curent; ++i)
        {
            RmqItem st = rmq[p - 1][i];
            if (i + (1 << (p - 1)) <= p_curent)
            {
                RmqItem dr = rmq[p - 1][i + (1 << (p - 1))];
                rmq[p][i] = st.nvl < dr.nvl ? st : dr;
            }
            else
            {
                rmq[p][i] = st;
            }
        }
    }
}

Pentru a raspunde la o interogare in $O(1)$ trebuie sa precalculam pentru o lungime oarecare de interval care este cea mai mare putere a lui $2$ mai mica sau egala cu ea.

int max_bit[2 * MAX_N];

void calculeaza_max_bit()
{
    // calculeaza max_bit[i] cea mai mare putere a lui 2 <= i
    max_bit[1] = 0;
    for (int i = 2; i <= p_curent; ++i)
    {
        max_bit[i] = max_bit[i / 2] + 1;
    }
}

Implementarea functiei lca poate fi realizata acum astfel:

int lca(int x, int y)
{
    int pos_x = p_start[x];
    int pos_y = p_start[y];
    if (pos_x > pos_y)
    {
        swap(pos_x, pos_y);
    }
    int p = max_bit[pos_y - pos_x + 1];
    RmqItem st = rmq[p][pos_x];
    RmqItem dr = rmq[p][pos_y - (1 << p) + 1];
    if (st.nvl < dr.nvl)
    {
        return st.nod;
    }
    else
    {
        return dr.nod;
    }
}

O implementare completa a acestei solutii puteti gasi aici.

Probleme

Pirati (infoarena)

Numim zona conexa orice submultime maximala de celule ce contin doar apa, respectiv pamant, si se poate ajunge de la orice celula la orice alta celula mergand doar pe apa, respectiv pe pamant.

Consideram un graf in care fiecare astfel de zona conexa reprezinta un nod, iar muchiile reprezinta faptul ca cele doua zone au cel putin o pereche de celule adiacente in matricea initiala.

Exemplu (bazat pe matricea din exemplul problemei):

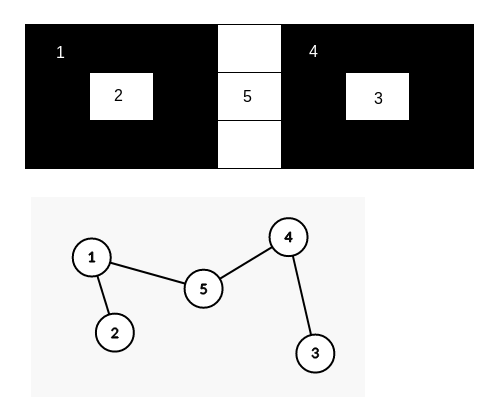
Se poate demonstra (usor intuitiv, putin mai dificil formal) ca acest graf este intotdeauna un arbore.

In mod evident toate muchiile unesc o zona de pamant (insula) cu o zona de apa. Deci pentru doua insule, numarul minim de insule ce trebuie parcurse pentru a ajunge de la una la cealalta se poate determina direct din lungimea lantului dintre nodurile lor corespunzatoare din arbore (nr_insule = (lungime + 1) / 2).

Determinarea zonelor conexe se poate realiza folosind un algoritm de tip fill sau folosind o parcurgere BF pornind din fiecare celula inca nevizitata si marcand toate celulele conexe de acelasi fel (apa/pamant).

Pentru determinarea lungimii drumurilor avem nevoie de LCA.

Consideram conform restrictiilor ca $O(N) = O(M)$. Observam ca adancimea maxima a arborelui corespunzator matricii de la intrare este $O(N)$. Cu alte cuvinte, ne permitem sa calculam LCA cu algoritmul brut care “urca” nodurile iterativ cu cate un nivel, in $O(N)$.

Puteti gasi aici o sursa in complexitate $O(N^2 + NQ)$.

CT (infoarena)

Problema ne cere sa determinam numarul minim de noduri pe care sa le stergem dintr-un arbore astfel incat pentru oricare pereche de noduri din input, cele doua noduri ale ei sa ajunga deconectate.

Pentru a deconecta nodurile x si y trebuie sa eliminam cel putin un nod de pe lantul unic dintre ele. Observam ca acest lant are doua parti “ascendente”: de la x la LCA(x, y) si de la y la LCA(x, y).

Consideram perechea de noduri din input (x, y) cu proprietatea ca are nivelul LCA(x, y) maxim dintre toate perechile. Fie z un nod oarecare de pe lantul de la x la y. Daca eliminam z cele doua noduri vor deveni deconectate, si, mai mult, vom deconecta intreg subarborele lui z de restul arborelui. Suntem obligati sa facem o eliminare intrucat cele doua noduri nu pot fi deconectate altfel (conform modului in care le-am ales).

Intrucat am ales perechea cu LCA pe nivel maxim, nu exista nicio alta pereche cu ambele noduri in subarborele lui z. Cu alte cuvinte, daca cumva in subarborele lui z avem un nod din vreuna din celelalte perechi din input, acum si acea pereche este deconectata. Devine clar acum ca ne-am dori sa alegem z care corespunde unui subarbore cat mai mare, pentru a avea sansa de a deconecta cat mai multe alte perechi. Dar acest z este chiar LCA(x, y).

Se contureaza urmatorul algoritm:

• sorteaza perechile de noduri (x, y) descrescator dupa nivelul LCA(x, y)
• pentru perechea curenta (x, y), daca x sau y este marcat ca “deconectat”, nu avem nimic de facut (a fost deja eliminat un nod care a deconectat x de y)
• altfel, vom elimina din arbore nodul LCA(x, y) si vom marca intregul subarbore al acestuia ca “deconectat”.

Pentru a obtine complexitatea optima, marcarea nodurilor ca “deconectat” se face printr-o parcurgere DF in care ne oprim cand ajungem intr-un nod marcat anterior (stim oricum ca intregul lui subarbore este de asemenea marcat deja):

void deleteNode(int node) {
	deleted[node] = true;
	for (int adj : tree[node]) {
		if (deleted[adj])
			continue;
		deleteNode(adj);
	}
}

Iar actualizarea solutiei, parcurgand perechile (x, y) in ordinea sortarii dupa LCA, arata astfel:

if (!deleted[x] && !deleted[y])
{
    deleteNode(LCA(x, y));
    sol++;
}

Folosind algoritmul optim pentru LCA, complexitatea finala este $O(N \log N + K)$.
Puteti consulta aici detaliile de implementare.

Atac (infoarena)

Problema ne cere sa raspundem la interogari pentru determinarea muchiei de cost minim aflata pe lantul dintre doua noduri oarecare dintr-un arbore.

Avantajul pe care il avem este ca arborele nu se modifica (daca am avea si update-uri atunci problema ar fi ceva mai grea, si ar trebui sa apelam la tehnici mai avansate - vezi Heavy Path Decomposition).

Ne vom inspira din solutia la problema LCA folosind “stramosi”. Pe langa tabela stramos mai putem calcula si o tabela:
cost[p][nod] := costul minim al unei muchii aflate pe lantul de la nod pana la stramos[p][nod].

Calculul celor doua tabele se poate face in paralel:

for (int i = 1; i < MAX_LOG; ++i)
{
    for (int j = 1; j <= n; ++j)
    {
        cost[i][j] = min(cost[i - 1][j], cost[i - 1][stramos[i - 1][j]]);
        stramos[i][j] = stramos[i - 1][stramos[i - 1][j]];
    }
}

Fie acum x, y doua noduri si z = LCA(x, y). Putem determina acum usor care este costul minim al unei muchii de la x la z, sau de la y la z:

int diff = nivel[x] - nivel[z];
for (int p = MAX_LOG - 1; p >= 0; --p)
{
    if (diff >= (1 << p))
    {
        diff -= (1 << p);
        minimum = min(minimum, cost[p][x]);
        x = stramos[p][x];
    }
}

Complexitatea acestei solutii este $O(N\log N + M\log N)$, de la precalcularea stramosilor si raspunsul la query-urile de LCA si cost minim in $O(\log N)$.

O implementare completa a acestei solutii puteti gasi aici.

Concurs (infoarena)

Aceasta problema este o aplicatie simpla a algoritmului de determinare a LCA pentru mai multe perechi de noduri. De aceasta data trebuie doar sa calculati maximul dintre valorile asociate LCA-urilor determinate.

O solutie in $O(N \log N + M)$ gasiti aici.

Probleme suplimentare

Delay (infoarena)

Hint 1: Daca mentinem pentru fiecare nod suma timpilor de la radacina pana la el, raspunsul pentru o interogare $(x, y)$ este: suma timpilor pentru $x$ $+$ suma timpilor pentru $y$ $-$ de doua ori suma timpilor pana la parintele LCA-ului.

Hint 2: La un update pentru timpul unui nod, se vor modifica toate sumele calculate pentru nodurile din subarborele sau. Daca consideram liniarizarea arborelui, operatia devine update pe interval.

Maxdist (infoarena)

Hint 1: Problema este simetrica pentru cele doua bande. Se cere mereu diametrul unui arbore din care fie se elimina frunze (prima banda), fie se adauga frunze (a doua banda). Este mai simpla adaugarea.

Hint 2: Cum se modifica diametrul intr-un arbore in care mai adaugam o frunza? Ce se pastreaza? Observati ce se intampla cu capetele diametrului original.