Elemente de Combinatorica 2.0

autor: Bogdan Iordache

Inainte de a parcurge acest material va recomand sa consultati articolul introductiv de aici.

Invers Modular

Incepem cu cateva notatii utile. Fie $a$ si $b$ doua numere intregi, iar $m$ un numar natural nenul. Folosim notatia $a \equiv b\ (mod\ m)$ cu semnificatia ca restul impartirii numarului $a$ la $m$ este egal cu restul impartirii numarului $b$ la $m$.

Pentru un numar $a$ intreg si $m$ natural nenul, definim inversul modular al lui $a$ in raport cu $m$, notat cu $a^{-1}$, ca fiind un numar natural din invervalul $[1, m-1]$ cu proprietatea ca: $a \cdot a^{-1} \equiv 1\ (mod\ m)$.

Determinarea inversului modular este utila in momentul in care vrem sa determinam restul impartirii la $m$ al unei formule care implica operatii de impartire. Spre exemplu, fie $a$ si $b$ doua numere intregi, cu proprietatea ca $b | a$. Presupunem ca $a'$ si $b'$ sunt resturile impartirii lui $a$, respectiv $b$ la $m$. Cunoscand $a'$ si $b'$ vrem sa determinam restul impartirii numarului $\frac{a}{b}$ la $m$ (il vom nota cu $r$). Aceasta problema o putem rezolva astfel:

$\frac{a}{b} \equiv r\ (mod\ m) \implies a \equiv r \cdot b\ (mod\ m) \implies$
$\implies a \cdot b^{-1} \equiv r \cdot b \cdot b^{-1}\ (mod\ m) \implies a' \cdot b'^{-1} \equiv r\ (mod\ m)$.

Tot ce trebuie sa facem este sa inmultim restul lui $a$ ($a'$) cu inversul modular al lui $b$ (care este usor de vazut ca este si inversul modular al lui $b'$).

Obs. Nu intotdeauna inversul modular exista. De exemplu, care este inversul modular al lui $2$ in raport cu $4$? Nu exista niciun numar pe care l-as putea inmulti cu $2$ astfel incat sa obtin un multiplu de $4$ plus $1$. O conditie necesara ca un numar $a$ sa accepte invers modular in raport cu $m$ este ca $(a, m) = 1$ (sa fie prime intre ele). Dem: Presupunem ca $a$ accepta invers modular, notat cu $a^{-1}$, notam cu $d = (a, m)$. Avem ca $d|a$ $\implies$ $d|a \cdot a^{-1}$ $\implies$ $d|k \cdot m + 1$ (divide un multiplu de $m$ plus $1$). Dar $d|m$, obtinem prin scaderea ultimelor doua relatii ca $d|1$, deci singura optiune este $(a, m) = 1$.

Conditia demonstrata mai devreme este necesara ($a$ si $m$ trebuie sa fie prime intre ele pentru a gasi invers modular), dar este oare si suficienta (daca $a$ si $m$ sunt prime intre ele, avem invers modular pentru $a$)? Raspunsul este da, si reiese usor din Teorema lui Euler:
$a^{\phi(m)} \equiv 1\ (mod\ m)$ daca $(a, m) = 1$; unde $\phi(m)$ este “indicatorul lui Euler” definit ca numarul de numere naturale mai mici decat $m$ care sunt prime cu $m$.

Rescriind formula de mai sus putem extrage o formula pentru $a^{-1}$, anume:
$a^{-1} \equiv a^{\phi(m) - 1}\ (mod\ m)$.

Obs. daca $m$ este prim, din moment ce $\phi(m) = m-1$, Teorema lui Euler ne da aceeasi relatie ca Mica Teorema a lui Fermat: $a^{m-1}\equiv 1\ (mod\ m)$, oricare ar fi $m$ prim si $a$ numar natural nedivizibil cu $m$.

Cum calculam $\phi(m)$ ?

Fie $p_1^{t_1} \cdot p_2^{t_2} \cdot \ldots \cdot p_k^{t_k}$ descompunerea in factori primi a lui $m$. Indicatorul lui Euler poate fi calculat astfel:
$$\phi(m) = m(1 - \frac{1}{p_1})(1 - \frac{1}{p_2})\ldots(1 - \frac{1}{p_k})$$.

Pentru un $m$ oarecare putem determina in $O(\sqrt{m})$ descompunerea in factori primi a acestuia si sa calculam indicatorul cu formula de mai sus. Daca vrem sa aflam indicatorul pentru mai multe numere, de exemplu pentru toate numerele naturale mai mici sau egale cu $N$, putem apela la o metoda de tip ciur:

for (int i = 1; i <= N; ++i)
	phi[i] = i;
for (int i = 2; i <= N; ++i) {
	if (phi[i] == i) {  \\ phi[i] nu a fost modificat, i este prim
		for (int j = i; j <= N; j += i)
			phi[j] = phi[j] / i * (i - 1);
	}
}

Cum calculam $a^{-1}$ ?

Pentru a calcula $a^{-1}$ avem de determinat restul impartirii lui $a^{\phi(m) - 1}$ la $m$. Acest lucru poate fi facut usor folosind exponentiere in timp logaritmic (complexitate $O(log\ m))$:

int log_pow(int a, int n, int mod) {
	// calculeaza a^n % mod
	int res = 1;
	while (n) {  // scriem n in baza 2
		if (n % 2 == 1)  // daca bitul curent este 1
			res = (res * a) % mod;  // inmultim la rezultat puterea de forma a^(2^k)
		n /= 2;
		a = (a * a) % mod;  // iteram prin a, a^2, a^4, a^8, ...
	}
	return res;
}

Daca cunoastem phi_m, indicatorul lui Euler pentru $m$, implementarea inversului modular se reduce la:

int inv_mod(int a, int m, int phi_m) {
	return log_pow(a, phi_m - 1, m);
}

Calculul formulelor combinatorice

Am vazut in articolul anterior cum calculul formulelor pentru combinari, aranjamente, etc. are ca principala dificultate evitarea impartirilor de factoriale. Putem acum sa ne folosim de notiunea de invers modular. Mai intai precalculam toate factorialele de care am putea avea nevoie:

fact[0] = 1;
for (int i = 1; i <= N; ++i)
	fact[i] = (i * fact[i - 1]) % MOD;

Putem calcula acum inversele modulare ale acestor factoriale. Putem eficientiza procesul folosindu-ne de faptul ca $(n-1)!^{-1} \equiv n \cdot n!^{-1}\ (mod\ MOD)$:

inv_fact[N] = inv_mod(fact[N], MOD, phi_MOD);
for (int i = N - 1; i; --i)
	inv_fact[i] = (i + 1) * inv_fact[i + 1] % MOD;

Putem acum, spre exemplu, sa calculam $C_i^j$ astfel:

int comb_i_j = fact[i] * inv_fact[j] * inv_fact[i - j] % MOD;

Obs. Pentru a putea calcula aceste inverse modulare trebuie ca $MOD$ sa fie prim cu toate factorialele precalculate. Deobicei, in probleme, $MOD$ este un numar prim $> N$, ceea ce garanteaza aceasta restrictie. Daca nu este valabila aceasta conditie, se pot face diverse artificii pentru a precalcula factorialele ignorand factorii primi din descompunerea acestora care il divid pe $MOD$, si calcularea separata a exponentilor acestora, puteti gasi o interpretare a acestei idei aici.

Problema 1 (Nozero)

Observația principală care ne duce la rezolvarea problemei este că numărul K este mic în comparație cu numărul total de permutări de ordin $N$ ($N!$). De aceea pentru orice $N \geq 13$ și orice $K \leq 10^9$ , primele $N-13$ poziții vor fi fixate (avem valoarea egală cu poziția) și doar ultimele cel mult $13$ valori vor fi permutate.

Astfel ajungem la următoarele subprobleme:

Subproblema 1: determinam a $K$-a permutare în ordine lexicografică de dimensiune cel mult $13$ (notăm această dimensiune cu $M$). Această subproblemă se poate rezolva în mai multe moduri întrucât lungimea permutărilor este mică. O variantă ar fi să încercăm să fixăm pe rând de la stânga la dreapta valorile. Pentru poziția $i$ încercăm în ordine crescătoare toate valorile care nu au fost puse încă, dacă o fixăm pe aceasta știm că elementele din dreapta ei pot fi permutate în $(M-i)!$ moduri. Dacă numărul de moduri în care mai putem permuta ultimele $M-i$ valori este mai mic decât $K$, scădem din $K$ acest număr și încercăm o valoare mai mare pe poziția $i$. La final vom avea toate valorile setate, iar K = 0.

Subproblema 2: determinarea numărului de valori care conțin cifra $0$ și sunt mai mici sau egale decât un P dat. Deoarce știm că primele aproximativ $N-13$ valori (al căror număr îl vom nota cu $P$) sunt egale cu poziția lor din permutare, este suficient să număram câte dintre aceste valori conțin $0$. Pentru un număr de cifre $c$ fixat avem $9^c$ valori de $c$ cifre care nu conțin cifra $0$. Cu această relație numărăm toate valorile care au numărul de cifre strict mai mic decât numărul de cifre ale lui $P$.
Mai avem de numărat valorile care au același număr de cifre cu $P$ si nu conțin $0$. Fiind mai mici decât $P$ și având același număr de cifre, putem grupa aceste valori după lungimea celui mai lung prefix pe care îl au în comun cu $P$. Dacă acest prefix conține 0 nu avem ce număra, iar dacă nu, vedem câte cifre nenule mai mici strict decât cifra de pe poziția imediat următoare prefixului din $P$ există, iar pentru fiecare din aceste variante celelalte cifre pot fi fixate cu oricare dintre cele $9$ valori nenule posibile.

Din cele două subprobleme putem determina câte poziții sunt valide (poziția nu conține cifra $0$ si valoarea de la acea poziție nu conține $0$).

Teorema lui Lucas

Fie $P$ un numar prim. Vrem sa calculam $C_N^M\ \%\ P$ (unde $N \geq M$). Observati ca nu am dat nicio restrictie suplimentara pentru $N$ si $M$, deci aceste valori pot fi mai mari decat $P$. Ne lovim deci de problema enuntata mai devreme, in care nu putem calcula direct inversele modulare ale factorialelor, intrucat acestea pot fi divizibile cu $P$.

Teorema lui Lucas ne vine in ajutor. Mai intai scriem numerele $N$ si $M$ in baza $P$:
$N = n_k\cdot{P^k} + n_{k-1}\cdot{P^{k-1}} + \ldots + n_1\cdot{P^1} + n_0$
$M = m_k\cdot{P^k} + m_{k-1}\cdot{P^{k-1}} + \ldots + m_1\cdot{P^1} + m_0$
$n_k > 0$; $0 \leq n_i, m_i < P$
Conform teoremei avem:
$$C_N^M \equiv \prod_{i=1}^k C_{n_i}^{m_i}\ (mod\ P)$$
cu conventia ca $C_{n_i}^{m_i} = 0$, daca $n_i < m_i$.

$C_{n_i}^{m_i}$ poate fi calculat usor, intrucat formula sa depinde de factoriale $< P!$, care sunt deci prime cu $P$.

Problema 2 (Jap2)

Aceasta problema se poate rezolva usor folosind direct Teorema lui Lucas.
Pentru o alta varianta de rezolvare, care se poate generaliza si la calculul de aranjamente, puteti consulta descrierea oficiala.

Problema 3 (Nmult)

Plecam de la faptul ca $x_{i+1} - x_i > w - 1$.
Realizam urmatoarea “schimbare de variabila”: $y_i = x_i - (i - 1)(w - 1)$.
$y_{i+1} - y_i = x_{i+1} - x_i - (w - 1) > 0$
Avem deci o bijectie (corespondenta una-la-unu) intre sirurile corecte $x_1, \ldots, x_k$ si sirurile $y_1, \ldots, y_k$, cu $1 \leq y_1 < y_2 < \ldots < y_k \leq n - (k-1)(w-1)$.

Am redus problema la a determina “cate siruri strict crescatoare de $k$ numere naturale din intervalul $[1, n - (k-1)(w-1)]$ exista”. R: $C_{n-(k-1)(w-1)}^{k}$.

Intrucat aceste combinari trebuie calculate modulo $666013$ (numar prim), iar $n, k, w \leq 10^6$, trebuie sa folosim teorema lui Lucas pentru a calcula combinarea.

Numere Catalan

Numerele catalan se noteaza cu $C_n$ si se calculeaza dupa formula $C_n = \frac{1}{n+1} C_{2n}^n$.

Acestor numere le este asociata o multime variata de clase de probleme care se reduc la calcularea formulei specificate. Enumeram doar cateva dintre acestea.

a. Numarul de siruri corecte de paranteze

Consideram un sir de $2n$ caractere, in care $n$ caractere sunt ‘$($’, iar celelalte sunt ‘$)$’. O parantezare corecta $P$ este un astfel de sir care respecta urmatoarea definitie recursiva:

• sirul vid este o parantezare corecta
• daca $P_1$ si $P_2$ sunt parantezari corecte, concatenarea lor este o parantezare corecta
• daca $P$ este o parantezare corecta, atunci $(P)$ este de asemenea o parantezare corecta.

Exemplu: $(())()$, $((()))$, $()()()$ sunt parantezari corecte, in timp ce $)(())($, $(()))$ nu sunt.

Numarul de parantezari corecte de lungime $2n$ este $C_n$.

b. Numarul de drumuri monotone in spatiu laticeal care nu depasesc diagonala principala

Consideram un spatiu laticeal (craoiaj) de dimensiune $n \times n$. Pornim din punctul $(0, 0)$ si dorim sa ajungem in $(n, n)$ facand pasi de lungime $1$ unitate fie in sus, fie la dreapta, cu conditia ca niciodata sa nu depasim diagonala principala, adica sa nu ajungem intr-un punct $(i, j)$ cu $i < j$. Cate astfel de drumuri se pot forma? R: $C_n$.

Avem mai jos toate drumurile posibile pentru $n=4$:

c. Numarul de arbori binari stricti

Un arbore binar strict este un arbore in care toate nodurile interne (care nu sunt frunze) au exact $2$ fii. Pentru un arbore binar strict cu $n$ noduri interne vom avea mereu $n+1$ frunze. Numarul de arbori binari stricti cu $n$ noduri interne este $C_n$.

Pentru $n=3$ avem urmatorii arbori:

d. Numarul de triangulari ale unui poligon convex

O triangulare a unui poligon convex reprezinta o modalitate de a trasa diagonale ale acestuia care nu se intersecteaza (cu exceptia capetelor) cu scopul de a imparti suprafata acestui poligon in triunghiuri. Pentru un poligon convex cu $n+2$ laturi avem $C_n$ triangulari.

Triangularile pentru un hexagon sunt urmatoarele:

Demonstratia formulei

Putem demonstra pentru oricare dintre problemele de mai sus ca numarul de posibilitati este $C_n$, apoi sa demonstram ca aceste probleme sunt echivalente intre ele. Vom schita pe scurt demonstratia ca numarul de drumuri sus-dreapta, care nu depasesc diagonala principala intr-un caroiaj de $n \times n$ este $C_n$. Pentru alte demonstratii puteti consulta articolul de pe Wikipedia.

Putem porni de la a numara toate drumurile sus-dreapta de la $(0, 0)$ la $(n, n)$. Acestea sunt in total $C_{2n}^{n}$ (orice astfel de drum trebuie sa contina $n$ pasi in sus si $n$ pasi la dreapta, interclasati in orice mod posibil).

Trebuie sa scadem acum drumurile care depasesc diagonala principala. Pentru a le numara pe acestea folosim urmatoarea metoda: fie un astfel de drum “gresit”, consideram primul punct de pe drum de forma $(i, j)$ cu $i < j$ (prima oara cand drumul depaseste diagonala principala). Numim diagonala critica, diagonala paralela cu cea principala aflata cu o unitate deasupra acesteia, evident $(i, j)$ se afla pe diagonala critica. Aplicam o reflexie a sufixului drumului incepand de la $(i, j)$ fata de diagonala critica. Obtinem astfel, in final, un drum de la $(0, 0)$ la $(n-1, n+1)$.

Exemplu de reflexie:

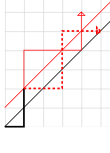
Este usor de vazut ca avem o bijectie de la drumurile “gresite” catre toate drumurile de la $(0, 0)$ la $(n-1, n+1)$. Un drum oarecare de la $(0, 0)$ la $(n-1, n+1)$ va trece cu siguranta peste diagonala principala si aplicand din nou operatia de reflexie ajungem la drumul “gresit” corespunzator. Obtinem astfel ca avem $C_{2n}^{n-1}$ drumuri “gresite”.

In final, $C_n = C_{2n}^n - C_{2n}^{n-1} = \frac{1}{n+1} C_{2n}^n$.

In continuare, vom da cateva exemple de demonstratii de echivalenta:

i) drumuri sus-dreapta sub diagonala principala $\Leftrightarrow$ siruri corecte de paranteze

Pornim de la urmatoarea observatie, un sir de paranteze este corect daca si numai daca:

• numarul de paranteze deschise este egal cu numarul de paranteze inchise
• pentru orice prefix, numarul de paranteze deschise este mai mare sau egal cu numarul de paranteze inchise

Putem construi acum urmatoarea bijectie: pentru un drum, marcam toti pasii la dreapta cu $($ si toti pasii in sus cu $)$. Intrucat drumul nu depaseste diagonala principala, pentru niciun prefix nu vom avea mai multe drumuri in sus decat la dreapta, deci orice sir de paranteze astfel obtinut este corect.

ii) siruri corecte de paranteze $\Leftrightarrow$ arbori binari stricti

Intr-un arbore binar strict, odata fixata configuratia nodurilor interne, pozitia frunzelor este unic determinata. Putem realiza o bijectie intre parantezari si arbori astfel:

• consideram prima paranteza deschisa si perechea sa (paranteza care “o inchide”): obtinem parantezarea $(P_1)P_2$
• desenam radacina arborelui, apoi construim recursiv subarborele stang si pe cel drept
• subarborelui stang ii asociem sirul de paranteze $P_1$
• subarborelui drept ii asociem sirul de paranteze $P_2$

Folosind procedeul de mai sus obtinem configuratia nodurilor interne, ramane doar sa mai adaugam si frunzele (un singur mod posibil). Pentru arborii din figura de mai sus, parantezarile asociate ar fi, in ordine:
$$((())), (()()), (())(), ()(()), ()()()$$

Problema 4 (Catalan)

Simpla implementare a formulei numerelor Catalan.

Problema 5 (Puteri3)

Reamintim binomul lui Newton:
$$(x+y)^n = \sum_{k=0}^n C_n^k \cdot x^{n-k} \cdot y^k$$

Folosim urmatoarea notatie mai generala: $S(k, n) = \sum\limits_{i=1}^n i^k$.
$$S(k, n) = \sum_{i=1}^{n+1} (i-1)^k = n^k + \sum_{i=1}^{n} (i-1)^k$$
$$S(k, n) = n^k + \sum_{i=1}^{n} \sum_{j=0}^{k} C_k^j \cdot i^j \cdot (-1)^{k-j}$$
$$S(k, n) = n^k + \sum_{j=0}^{k} C_k^j \cdot (-1)^{k-j} \cdot S(j, n)$$
$$S(k, n) = n^k + S(k, n) + \sum_{j=0}^{k-1} C_k^j \cdot (-1)^{k-j} \cdot S(j, n)$$
$$n^k = -\sum_{j=0}^{k-1} C_k^j \cdot (-1)^{k-j} \cdot S(j, n)$$
Substituim $k$ cu $k+1$:
$$n^{k+1} = \sum_{j=0}^{k} C_{k+1}^j \cdot (-1)^{k-j} \cdot S(j, n)$$
$$n^{k+1} = (k+1) \cdot S(k, n) + \sum_{j=0}^{k-1} C_{k+1}^j \cdot (-1)^{k-j} \cdot S(j, n)$$
Obtinem formula pentru $S(k, n)$:
$$S(k, n) = \frac{1}{k+1} [n^{k+1} - \sum_{j=0}^{k-1} C_{k+1}^j \cdot (-1)^{k-j} \cdot S(j, n)]$$

Am obtinut deci o recurenta pentru $S(k, n)$ bazata pe $S(0, n), S(1, n), \ldots, S(k-1, n)$. Tinand cont ca $S(0, n) = n$, putem determina $S(k, n)$ in $O(k^2)$.

Problema 6 (Shgraf)

Definim $S[i]$ numarul de shgrafuri cu $i$ noduri, etichetate folosind $i$ etichete distincte. Un shgraf poate avea mai multe componente conexe, a caror ordine nu conteaza. Una dintre aceste componente conexe va contine nodul cu cea mai mare eticheta. Putem fixa $j$ dimensiunea acestei componente. Restul etichetelor din aceasta componenta pot fi alese in $C_{i-1}^{j-1}$ moduri. Obtinem recurenta:
$$S[i] = \sum_{j=1}^i C_{i-1}^{j-1} \cdot D[j] \cdot S[i - j]$$

Am notat cu $D[j]$ numarul de shgrafuri conexe cu $j$ noduri, etichetate folosind $j$ etichete distincte. Pentru a numara aceste shgrafuri observam mai intai ca structura lor corespunde unui ciclu de care sunt “agatati” arbori cu radacina in nodurile ciclului. Pentru $D[i]$, numarul de astfel de grafuri cu $i$ noduri, putem fixa mai intai structura ciclului. Putem fixa $j$ dimensiunea acestuia, avem la dispozitie $(j-1)! \cdot C_i^j$ moduri de a eticheta acest ciclu (alegem $j$ etichete si le permutam pe un ciclu de lungime $j$). Obtinem recurenta:
$$D[i] = \sum_{j=3}^{i} (j-1)! \cdot C_i^j \cdot A[j][i - j]$$

Am notat cu $A[i][j]$ numarul de moduri in care putem organiza $j$ noduri in arborii “agatati” de un ciclu cu $i$ noduri, etichetandu-le cu $j$ etichete distincte. Ciclul de $i$ noduri este deja fixat si etichetat, deci putem stabili o ordine a nodurilor de pe ciclu. Incercam sa fixam acum cate noduri vor fi agatate intr-un arbore cu radacina in ultimul nod de pe ciclu. Fie $k$ numarul acestora, putem sa le etichetam in $C_j^k$ moduri. Ramane acum sa determinam cati arbori etichetati cu $k+1$ noduri exista ($k$ nodurile alese, plus ultimul nod de pe ciclu). Numarul acestor arbori este $(k+1)^{k-1}$ (pentru demonstratie studiati Codurile Prüfer). Obtinem recurenta:
$$A[i][j] = \sum_{k=0}^{j} C_j^k \cdot (k+1)^{k-1}\cdot A[i-1][j-k]$$

Problema ne cere sa ignoram acele shgrafuri care au cicluri de lungime mai mica decat $K$. Putem “repara” recurenta pentru $D[i]$ considerand doar $j \geq K$. Obtinem complexitatea finala $O(N^3)$.

Problema 7 (provocare)

Pornim de la urmatoarea observatie: putem asocia fiecarui nod din arbore un sir de caractere de forma “aabbab” care descrie secventa de muchii de la radacina arborelui pana la acel nod. Evident, pentru oricare doua noduri distincte din arbore, sirurile de caractere asociate sunt diferite.

Vom incerca sa cautam binar inaltimea arborelui. Pentru o inaltime fixata numaram cate secvente de caractere corespund unei lungimi mai mici decat aceasta inaltime. Lungimea se calculeaza ca $x \cdot A + y \cdot B$ (unde $x$ si $y$ sunt numerele de caractere “a” si “b” din secventa, $A$ si $B$ au semnificatia din enunt). Daca numarul de astfel de secvente este mai mic decat $N$, inseamna cu certitudine ca inaltimea arborelui trebuie sa fie mai mare (“nu incap toate nodurile in aceasta inaltime”), daca numarul este $\geq N$ vom incerca o inaltime mai mica.

Stiind ca avem $x$ caractere “a” si $y$ caractere “b”, putem genera $C_{x+y}^x$ secvente. Numarul pe care incercam sa il determinam, pentru o inaltime fixata ($H$) in cautarea binara, este:
$$\sum_{x\cdot A + y\cdot B \leq H} C_{x+y}^x$$

Presupunem, fara a restrange generalitatea, ca $A \leq B$. Daca fixam $y$, valoarea maxima pentru $x$ este $x_{max} =[\frac{H - y\cdot B}{A}]$. Deci pentru $y$ fixat adunam la numarul posibil de noduri:
$$\sum_{x=0}^{x_{max}} C_{x+y}^x = \sum_{x=0}^{x_{max}} C_{x+y}^y$$.

Pentru a restrange expresia de mai sus, vom incerca o interpretare intuitiva a formulei. Amintim formula “stars and bars”: $C_{n+m-1}^{m-1} =$ numarul de moduri de a imparti $n$ bile identice in $m$ cutii diferite. Schimband notatiile $C_{x+y}^{y}$ reprezinta numarul de moduri de a distribui $x$ bile identice in $y+1$ cutii diferite. In concluzie, suma de mai sus se traduce in “cate moduri de a distribui cel mult $x_{max}$ bile identice in $y+1$ cutii diferite” exista. Dar acest lucru este echivalent cu a numara in cate moduri putem imparti $x_{max}$ bile in $y+2$ cutii (ultima cutie reprezinta bilele “aruncate”). Obtinem formula restransa:
$$\sum_{x=0}^{x_{max}} C_{x+y}^y = C_{x_{max} + y + 1}^{y + 1}$$.

Ultima optimizare vine din observatia ca foarte multe din combinarile de mai sus au valori mari. Pentru $n > 100$ si $k > 5$, avem $C_n^k > 10^9$. Deci daca ajungem la o astfel de combinare in timpul calculului, putem sa il oprim si sa stabilim ca inaltimea fixata este mai mare sau egala cu cea cautata.

Complexitatea finala va fi aproximativ $O(log\ H \cdot log\ N + C)$, unde $C$ este numarul de combinari care trebuie precalculate (in jur de $10.000$).

Relatii de recurenta. Calcul matriceal

Problema 8 (KFib)

Problema ne cere sa determinam al $K$-lea termen al sirului Fibonacci ($F_K$). Consideram urmatorul vector cu $2$ elemente: $\begin{pmatrix} F_{i-1} \\ F_i \end{pmatrix}$, continand doua numere consecutive din sirul Fibonacci. Printr-o inmultire cu o matrice de dimensiune $2 \times 2$, putem obtine vectorul continand termenii $F_i$ si $F_{i+1}$.

$$\begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} \cdot \begin{pmatrix} F_{i-1} \\ F_i \end{pmatrix} = \begin{pmatrix} F_i \\ F_{i-1} + F_i \end{pmatrix} = \begin{pmatrix} F_i \\ F_{i+1} \end{pmatrix}$$

Folosind proprietatea de asociativitate a inmultirii de matrici obtinem:
$$\begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix}^K \cdot \begin{pmatrix} F_{0} \\ F_1 \end{pmatrix} = \begin{pmatrix} F_K \\ F_{K+1} \end{pmatrix}$$

Putem determina deci $F_K$ in complexitate $O(log\ K)$ folosind metoda de ridicare la putere in timp logaritmic a matricei patratice. O implementare a acestei idei o puteti accesa aici.

Problema 9 (Iepuri)

Notam cu $I_n$ numarul de iepuri din ziua $n$.
$I_0=X$, $I_1=Y$, $I_2=Z$
$I_n = A*I_{n-1} + B*I_{n-2} + C*I_{n-3}$

Construim matricea $M = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ C & B & A \end{pmatrix}$
Avem: $\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ C & B & A \end{pmatrix} \cdot \begin{pmatrix} I_{n-3} \\ I_{n-2} \\ I_{n-1} \end{pmatrix} = \begin{pmatrix} I_{n-2} \\ I_{n-1} \\ I_{n} \end{pmatrix}$
Putem sa aplicam inca o data ridicarea la putere in timp logaritmic pentru formula:
$$\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ C & B & A \end{pmatrix}^{N} \cdot \begin{pmatrix} I_{0} \\ I_{1} \\ I_{2} \end{pmatrix} = \begin{pmatrix} I_{N} \\ I_{N+1} \\ I_{N+2} \end{pmatrix}$$

Problema 10 (Ecu)

Trecerea de la valorile de la iteratia $i$: ($x_1^{(i)}, x_2^{(i)}, \ldots, x_N^{(i)}$) la valorile de la itaratia $i+1$: ($x_1^{(i+1)}, x_2^{(i+1)}, \ldots, x_N^{(i+1)}$) se poate face printr-o inmultire cu o matrice de dimensiune $N \times N$.

Aplicand ridicare la putere in timp logaritmic obtinem complexitatea $O(N^3\ log\ M)$. Termenul $N^3$ vine de la complexitatea de a inmulti doua matrici de dimensiune $N \times N$.

Problema 11 (Recurenta2)

Notam $S_i = \sum\limits_{j=1}^i j \cdot X_j$. Recurenta pentru $S_{i+1} = S_{i} + (i+1) \cdot X_{i+1}$.

Il putem explicita pe $X_{i+1}$ in functie de termenii anteriori:
$S_{i+1} = S_{i} + (i+1) \cdot X_{i-1} \cdot B + (i+1) \cdot X_{i} \cdot A + (i + 1) \cdot C$.

Putem organiza aceasta recurenta folosind urmatoarea matrice:
$$\begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ B & A & C & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & B & A & C \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ B & A & C & 0 & B & A & C \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} X_{i-2} \\ X_{i-1} \\ 1 \\ S_{i-1} \\ i \cdot X_{i-2} \\ i \cdot X_{i-1} \\ i \end{pmatrix} = \begin{pmatrix} X_{i-1} \\ X_{i} \\ 1 \\ S_{i} \\ (i+1) \cdot X_{i-1} \\ (i + 1) \cdot X_{i} \\ i + 1 \end{pmatrix}$$
Putem sa determinam $S_N$ in $O(log\ N)$ folosind exponentiere in timp logaritmic de matrice.

Principiul includerii si excluderii

Fie $A, B, C, A_1, A_2, \ldots, A_n$ multimi finite. Principiul includerii si excluderii cuprinde urmatoarele identitati:

• $|A \cup B| = |A| + |B| - |A \cap B|$
• $|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|$
• $|\bigcup\limits_{i=1}^n A_i| = \sum\limits_{i=1}^n |A_i| - \sum\limits_{1\leq i < j \leq n} |A_i \cap A_j| + \sum\limits_{1\leq i < j < k \leq n} |A_i \cap A_j \cap A_k| - \ldots + (-1)^{n-1}|A_1 \cap A_2 \cap \ldots \cap A_n|$

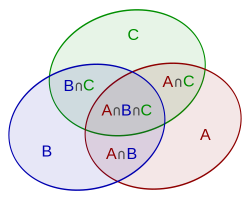
Problema 12 (Pinex)

Problema este o aplicatie simpla a principiului includerii si excluderii.
Fie $p_1, p_2, \ldots, p_n$ divizorii primi ai lui $B$.
Notam cu $M_i = \{x | 2 \leq x \leq A, p_i | x\}$ (multimea numerelor mai mici decat $A$, divizibile cu $p_i$).

Fie $X \leq A$, $X$ este prim cu $B$, adica $(X, B) = 1$, daca si numai daca $\forall i=\overline{1, n}$, $X$ nu este divizibil cu $p_i$. Putem deci observa ca numarul de numere prime cu $B$ mai mici decat $A$ este:

$$A - |A_1 \cup A_2 \cup \ldots \cup A_n|$$

Dar putem calcula $|A_1 \cup A_2 \cup \ldots \cup A_n|$ folosind principiul includerii si excluderii. Pentru aceasta trebuie sa stabilim care este cardinalul unei intersectii oarecare de astfel de multimi. Fie $1 \leq i_1 < \ldots < i_k \leq n$, $1 \leq k \leq n$, care este cardinalul multimii $|A_{i_1} \cap A_{i_2} \cap \ldots \cap A_{i_k}|$?

Ce inseamna ca un numar $X$ se afla in multimea $|A_{i_1} \cap A_{i_2} \cap \ldots \cap A_{i_k}|$? Inseamna ca $X$ se divide cu $p_{i_1}, \ldots, p_{i_k}$, dar toate aceste valori sunt numere prime, deci $X$ se divide si cu $p_{i_1} \cdot p_{i_2} \cdot \ldots \cdot p_{i_k}$.

Cate numere $\leq A$ se divid cu un numar $D$? $[\frac{A}{D}]$

Avem deci: $|A_{i_1} \cap A_{i_2} \cap \ldots \cap A_{i_k}| = [\frac{A}{p_{i_1} \cdot p_{i_2} \cdot \ldots \cdot p_{i_k}}]$.

Sirurile de indici $1 \leq i_1 < \ldots < i_k \leq n$, $1 \leq k \leq n$ pot fi generate in $O(2^n)$ folosind backtracking sau iterand prin toate numerele cu $n$ biti, urmand ca pentru o configuratie cardinalul intersectiei sa fie calculat in $O(n)$. Cum $n$ numarul de numere prime distincte care il divid pe $B$ este mic, solutia se incadreaza fara probleme in timp.

Problema 13 (Indep)

Notam cu $A$ sirul $A_1, \ldots, A_n$ din enunt.
Notam cu $VMAX$ valoarea maxima din $A$ ($VMAX \leq 1000$).
Notam cu $D_X = \{a | a\in A, X|a\}$ (multimea numerelor din $A$ divizibile cu $X$).
Notam cu $Z_X = 2^{|D_X|} - 1$, numarul de subsiruri nevide ale lui $A$ in care toate elementele sunt divizibile cu $X$.

Fie $p_1, \ldots,p_k$ toate numerele prime mai mici decat $VMAX$.
Un subsir al lui $A$ are cmmdc-ul $1$ daca si numai daca $\forall p_i, i=\overline{1, k}$ exista un element al subsirului care nu este divizibil cu $p_i$.

Folsind principiul includerii si excluderii, observam ca numarul cautat de subsiruri este:
$$R = Z_1 - Z_{p_1} - Z_{p_2} - \ldots - Z_{p_k} + Z_{p_1 \cdot p_2} + Z_{p_1 \cdot p_3} + \ldots + Z_{p_{k-1} \cdot p_k} - Z_{p_1 \cdot p_2 \cdot p_3} - \ldots$$

O complexitate de $O(2^k)$ ar fi prea mare pentru a obtine raspunsul. Insa observam ca ne intereseaza $Z_X$ doar pentru $X \leq VMAX$. Cu alte cuvinte ne uitam la toate numerele din intervalul $[1, VMAX]$ care se scriu ca produs de numere prime distincte. Daca $X$ se scrie ca un produs de un numar impar de numere prime distincte scadem din raspuns $Z_X$, iar daca se scrie ca un produs de un numar par de numere prime distincte adunam $Z_X$ la raspuns.

Ca o ultima observatie, intrucat $|D_X| \leq N \leq 500$, numerle $Z_X$ pot depasi orice tip intreg din C++, deci avem nevoie sa mentinem $Z_X$ folosind numere mari.

Problema 14 (Cowfood)

Numarul de experimente cautat il vom putea calcula ca $T-F$, unde $T$ reprezinta numarul total de experimente valide (valide in legatura cu limita $S$), iar $F$ reprezinta numarul de experimente valide care sigur vor esua.

Pentru un experiment $X$ notam $F_X$ multimea experimentelor care vor esua conform experimentului $X$. Astfel pentru un experiment $A = (a_1, \ldots, a_k)$, toate experimentele $B=(b_1, \ldots, b_k)$ cu $a_1 \leq b_1, a_2 \leq b_2, \ldots, a_k \leq b_k$ apartin multimii $F_A$.

Observam ca $F = |F_{E_1} \cup F_{E_2} \cup \ldots \cup F_{E_n}|$, unde $E_i$ sunt experimentele din input.
Folosind principiul includerii si excluderii: $F = |F_{E_1}| + |F_{E_2}| + \ldots + |F_{E_n}| - |F_{E_1} \cap F_{E_2}| - |F_{E_1} \cap F_{E_3}| - \ldots -|F_{E_{n-1}} \cap F_{E_n}| + \ldots + (-1)^{n-1}|F_{E_1} \cap \ldots \cap F_{E_n}|$.

Ce inseamna intersectia in acest context?
Daca $A=(a_1, \ldots, a_k)$ si $B=(b_1, \ldots, b_k)$ sunt doua experimente, $F_A \cap F_B$ corespunde multimii experimentelor care vor esua atat conform lui $A$ cat si conform lui $B$, echivalent cu a considera experimentele care vor esua conform experimentului $(max(a_1, b_1), max(a_2, b_2), \ldots, max(a_k, b_k))$.

Astfel pentru a calcula formula putem folosi backtracking pentru a genera toate submultimile de experimente din input si a reduce aceasta submultime la un singur experiment echivalent.

Ramane sa stabilim cum putem calcula $|F_X|$ pentru orice experiment $X=(x_1, \ldots, x_k)$. Pentru a obtine un experiment esuat putem incrementa oricare dintre valorile $x_i$ atata timp cat suma lor nu depaseste $S$. Deci putem realiza cel mult $S - (x_1 + \ldots + x_k)$ astfel de incrementari. Este echivalent cu a numara “in cate moduri pot distribui cel mult $S - (x_1 + \ldots + x_k)$ bile identice in $k$ cutii diferite”.

Am vazut la problema Provocare cum ca numarul de moduri de a distribui cel mult $i$ bile identice in $j$ cutii diferite este egal cu numarul de moduri de a distribui exact $i$ bile identice in $j+1$ cutii (ultima cutie reprezinta bilele pe care le “aruncam/ignoram”). Acest lucru se poate calcula folosind “stars and bars”: $C_{i+j}^j$.

Pentru a determina $T$, numarul total de experimente valide, putem determina $|F_{E_0}|$, unde $E_0 = (0, 0, \ldots, 0)$, adica cate experimente esueaza conform experimentului cu toate valorile $0$ (toate experimentele esueaza in acest caz).

Complexitatea asteptata este $O(K \cdot 2^N + S)$.

Bibliografie

• https://www.infoarena.ro
• https://wikipedia.org